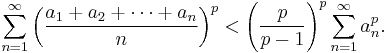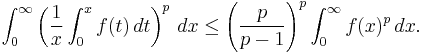Hardy's inequality
Hardy's inequality is an inequality in mathematics, named after G. H. Hardy. It states that if 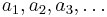 is a sequence of non-negative real numbers which is not identically zero, then for every real number p > 1 one has
is a sequence of non-negative real numbers which is not identically zero, then for every real number p > 1 one has
An integral version of Hardy's inequality states if f is an integrable function with non-negative values, then
Equality holds if and only if f(x) = 0 almost everywhere.
Hardy's inequality was first published (without proof) in 1920 in a note by Hardy.[1] The original formulation was in an integral form slightly different from the above.
See also
Notes
- ^ Hardy, G.H., Note on a Theorem of Hilbert, Math. Z. 6 (1920), 314–317.
References
- Hardy, G. H.; Littlewood. J.E.; Pólya, G. (1952). Inequalities, 2nd ed. Cambridge University Press. ISBN 0521358809.
- Kufner, Alois; Persson, Lars-Erik (2003). Weighted inequalities of Hardy type. World Scientific Publishing. ISBN 9812381953.
- Ribarič, M. (1973), "On some inequalities for convex functions", Mathematica Balkanica 3: 435–442.